জ্যামিতি গণিতের একটি গুরুত্বপূর্ণ শাখা যা বিন্দু, রেখা, তল, কোণ এবং আকৃতির ধারণা নিয়ে কাজ করে। বর্গ হলো জ্যামিতির একটি মৌলিক এবং নিখুঁত আকৃতি যা চারটি সমান দৈর্ঘ্যের বাহু এবং চারটি সমকোণ (90°) দ্বারা গঠিত। এই ব্লগ পোস্টে, আমরা বর্গের ধারণা, এর বৈশিষ্ট্য, পরিমাপ এবং কিছু গুরুত্বপূর্ণ প্রয়োগ নিয়ে আলোচনা করব।

Table of contents
বর্গ কাকে বলে?
বর্গের সঙ্গাঃ চারটি সমান দৈর্ঘ্যের বাহু এবং চারটি সমকোণ (90°) দ্বারা আবদ্ধ সমতল বদ্ধ স্থানকে বর্গ বলে। বর্গের বিপরীত বাহু সমান্তরাল হয় এবং সমস্ত কোণ সমকোণ (90°) হয়।
অন্যভাবেও বলা যায়, আয়তক্ষেত্রের দুটি সন্নিহিত বাহু যদি সমান হয় তখন তাকে বর্গ বলে।
বর্গের বৈশিষ্ট্য
বর্গের বৈশিষ্ট্যগুলো হলঃ
- সমস্ত বাহু সমান দৈর্ঘ্যের হয়।
- বর্গের দুটি সন্নিহিত বাহু সমান।
- বর্গের সবগুলো কোন সমান এবং সমস্ত কোণ সমকোণ (90°) হয়।
- বিপরীত বাহু সমান্তরাল হয়।
- কর্ণদ্বয় (দুটি বিপরীত কোণকে সংযোগকারী রেখা) পরস্পর সমান দৈর্ঘ্যের হয় এবং বর্গক্ষেত্রের ভেতর দিয়ে লম্বভাবে বিভক্ত করে।
- বর্গের ক্ষেত্রফল এবং পরিসীমা সহজে গণনা করা যায়।
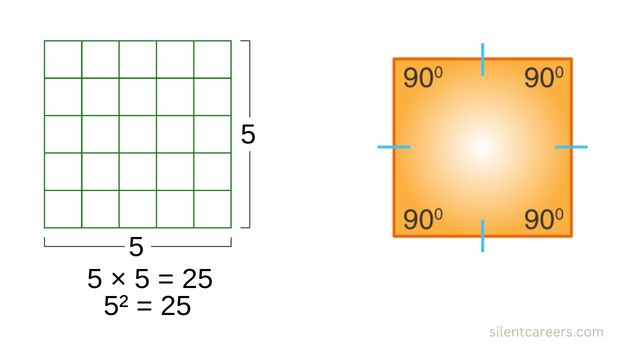
বর্গের পরিমাপ
- বর্গের বাহুর দৈর্ঘ্য (a) জানলে:
- ক্ষেত্রফল (A) = a * a
- পরিধি (P) = 4a
- কর্ণের দৈর্ঘ্য (d) = a * √2
- বর্গের ক্ষেত্রফল (A) জানলে:
- বাহুর দৈর্ঘ্য (a) = √A
- পরিধি (P) = 4√A
- কর্ণের দৈর্ঘ্য (d) = a * √2 = √2A
বর্গ ক্ষেত্রের সূত্রসমূহ
বর্গ ক্ষেত্র হলো এমন একটি চতুর্ভুজ যার চারটি বাহু সমান দৈর্ঘ্যের এবং চারটি কোণ সমকোণ (90°) হয়। বর্গ ক্ষেত্রের ক্ষেত্রফল, পরিসীমা, কর্ণের দৈর্ঘ্য ইত্যাদি নির্ণয়ের জন্য বিভিন্ন সূত্র ব্যবহার করা হয়।
১. বর্গ ক্ষেত্রের ক্ষেত্রফল
বর্গ ক্ষেত্রের ক্ষেত্রফল নির্ণয়ের সূত্র:
১। বাহুর দৈর্ঘ্য জানা থাকলে,
বর্গক্ষেত্রের ক্ষেত্রফল = বাহুর দৈর্ঘ্য (a) × বাহুর দৈর্ঘ্য (a) = a²
২। কর্ণ জানা থাকলে,
বর্গক্ষেত্রের ক্ষেত্রফল = (কর্ণ)2/2
উদাহরণ: ধরা যাক, একটি বর্গের বাহুর দৈর্ঘ্য 5 সেমি।
তাহলে, ক্ষেত্রফল = 5 সেমি × 5 সেমি = 25 বর্গ সেমি।
অর্থাৎ, এই বর্গ ক্ষেত্রের ক্ষেত্রফল 25 বর্গ সেমি।
২. বর্গ ক্ষেত্রের পরিসীমা
বর্গ ক্ষেত্রের পরিসীমা নির্ণয়ের সূত্র:
পরিসীমা = 4 × বাহুর দৈর্ঘ্য (a) = 4a
উদাহরণ: ধরা যাক, একটি বর্গের বাহুর দৈর্ঘ্য 5 সেমি।
তাহলে, পরিসীমা = 4 × 5 সেমি = 20 সেমি।
অর্থাৎ, এই বর্গ ক্ষেত্রের পরিসীমা 20 সেমি।
৩. বর্গ ক্ষেত্রের কর্ণের দৈর্ঘ্য
বর্গ ক্ষেত্রের কর্ণের দৈর্ঘ্য নির্ণয়ের সূত্র:
কর্ণ = বাহুর দৈর্ঘ্য (a) × √2
উদাহরণ: ধরা যাক, একটি বর্গের বাহুর দৈর্ঘ্য 5 সেমি।
তাহলে, কর্ণ = 5 সেমি × √2 ≈ 7.07 সেমি।
অর্থাৎ, এই বর্গ ক্ষেত্রের কর্ণের দৈর্ঘ্য প্রায় 7.07 সেমি।
৪. বর্গ ক্ষেত্রের একটি কোণের পরিমাণ:
বর্গ ক্ষেত্রের একটি কোণের পরিমাণ নির্ণয়ের সূত্র:
একটি কোণের পরিমাণ = 360° / 4 = 90°
এই সূত্র থেকে বোঝা যায় যে, বর্গ ক্ষেত্রের প্রতিটি কোণ সমকোণ (90°) হয়।
৫. বর্গ ক্ষেত্রের অভ্যন্তরীণ কোণের সমষ্টি:
বর্গ ক্ষেত্রের অভ্যন্তরীণ কোণের সমষ্টি নির্ণয়ের সূত্র:
অভ্যন্তরীণ কোণের সমষ্টি = n × (n – 2) × 180° = 4 × (4 – 2) × 180° = 360°
বর্গ সম্পর্কিত কিছু প্রশ্ন (FAQ)
১. বর্গ কী?
উত্তর: বর্গ হলো এমন একটি চতুর্ভুজ যার চারটি বাহু সমান দৈর্ঘ্যের এবং চারটি কোণ সমকোণ (90°) হয়।
২. বর্গের বৈশিষ্ট্য কী কী?
উত্তর:
- সমস্ত বাহু সমান দৈর্ঘ্যের।
- বিপরীত বাহু সমান্তরাল।
- সমস্ত কোণ সমকোণ (90°)।
- কর্ণের দৈর্ঘ্য √2a (a হলো বাহুর দৈর্ঘ্য)।
- অভ্যন্তরীণ কোণের সমষ্টি 360°।
৩. বর্গ ক্ষেত্রের ক্ষেত্রফল কীভাবে বের করবেন?
উত্তর: বর্গ ক্ষেত্রের ক্ষেত্রফল নির্ণয়ের জন্য, নিম্নলিখিত সূত্র ব্যবহার করুন:
ক্ষেত্রফল = বাহুর দৈর্ঘ্য (a) × বাহুর দৈর্ঘ্য (a) = a²
৪. বর্গ ক্ষেত্রের পরিসীমা কীভাবে বের করবেন?
উত্তর: বর্গ ক্ষেত্রের পরিসীমা নির্ণয়ের জন্য, নিম্নলিখিত সূত্র ব্যবহার করুন:
পরিসীমা = 4 × বাহুর দৈর্ঘ্য (a) = 4a
৫. বর্গ ক্ষেত্রের কর্ণের দৈর্ঘ্য কীভাবে বের করবেন?
উত্তর: বর্গ ক্ষেত্রের কর্ণের দৈর্ঘ্য নির্ণয়ের জন্য, নিম্নলিখিত সূত্র ব্যবহার করুন:
কর্ণের দৈর্ঘ্য = বাহুর দৈর্ঘ্য (a) × √2
৬. বর্গ ক্ষেত্রের কোন কোন ক্ষেত্রে বিশেষ সূত্র ব্যবহার করে ক্ষেত্রফল বের করা যায়?
উত্তর: বর্গ ক্ষেত্রের ক্ষেত্রফল নির্ণয়ের জন্য অন্য কোন বিশেষ সূত্র প্রয়োজন হয় না।
৭. দৈনন্দিন জীবনে আমরা কিভাবে বর্গ দেখতে পাই?
উত্তর: বর্গ আমাদের চারপাশে সর্বত্রই রয়েছে। উদাহরণ:
- দেয়ালের টাইলস
- খেলার কার্ড
- কিছু ছবির ফ্রেম
৮. জ্যামিতিতে বর্গের গুরুত্ব কী?
উত্তর: বর্গ জ্যামিতির একটি মৌলিক ধারণা। এটি আরও জটিল আকার যেমন ঘনক, প্রিজম, এবং পিরামিড বোঝার ভিত্তি স্থাপন করে। বর্গের বৈশিষ্ট্য এবং সূত্রগুলি এলাকা এবং পরিধি নির্ণয়ে সাহায্য করে।
৯. উচ্চতর গণিতে বর্গের কি কোনো ব্যবহার আছে?
উত্তর: হ্যাঁ, উচ্চতর গণিতে বর্গের বিভিন্ন ধারণা ব্যবহার করা হয়। উদাহরণস্বরূপ, ক্যালকুলাসে এলাকা এবং পরিধি নির্ধারণের সময় বর্গের সমীকরণ ব্যবহার করা হয়। টপোলজি নামক গণিতের শাখায়ও বর্গের ধারণা গুরুত্বপূর্ণ।
বর্গ সম্পর্কিত কিছু বহুনির্বাচনী প্রশ্নোত্তর
১. নিম্নলিখিত কোন ধরণের চতুর্ভুজের সমস্ত বাহু সমান দৈর্ঘ্যের এবং সমস্ত কোণ সমকোণ (90°) হয়?
(a) ট্র্যাপিজিয়াম (b) আয়তক্ষেত্র (c) রম্বস (d) বর্গ
উত্তর: (d) বর্গ
২. একটি বর্গের ক্ষেত্রফল নির্ণয়ের জন্য, আমরা কোন সূত্র ব্যবহার করব?
(a) ½ × (ভিত্তি × উচ্চতা) (b) a × b (c) 4a (d) πr²
উত্তর: (b) a × b
৩. একটি বর্গের পরিসীমা নির্ণয়ের জন্য, আমরা কোন সূত্র ব্যবহার করব?
(a) ½ × (ভিত্তি × উচ্চতা) (b) a × b (c) 4a (d) πr²
উত্তর: (c) 4a
৪. একটি বর্গের কর্ণের দৈর্ঘ্য নির্ণয়ের জন্য, আমরা কোন সূত্র ব্যবহার করব?
(a) ½ × (ভিত্তি × উচ্চতা) (b) a × b (c) 4a (d) a√2
উত্তর: (d) a√2
৫. একটি বর্গের প্রতিটি কোণের পরিমাণ কত?
(a) 60° (b) 90° (c) 120° (d) 180°
উত্তর: (b) 90°
৬. একটি বর্গের অভ্যন্তরীণ কোণের সমষ্টি কত?
(a) 180° (b) 270° (c) 360° (d) 540°
উত্তর: (c) 360°
৭. নিম্নলিখিত কোনটি একটি বর্গের বৈশিষ্ট্য নয়?
(a) সমস্ত বাহু সমান দৈর্ঘ্যের (b) বিপরীত বাহু সমান্তরাল (c) সমস্ত কোণ সমকোণ (90°) (d) কর্ণের দৈর্ঘ্য √2a
উত্তর: (b) বিপরীত বাহু সমান্তরাল
৮. একটি বর্গের ক্ষেত্রফল 49 বর্গ ইউনিট। বর্গটির বাহুর দৈর্ঘ্য কত?
(a) 5 ইউনিট (b) 7 ইউনিট (c) 7 ইউনিট (d) 10 ইউনিট
উত্তর: (c) 7 ইউনিট
৯. একটি বর্গের পরিসীমা 28 ইউনিট। বর্গটির বাহুর দৈর্ঘ্য কত?
(a) 5 ইউনিট (b) 7 ইউনিট (c) 8 ইউনিট (d) 7 ইউনিট
উত্তর: (d) 7 ইউনিট
১০. একটি বর্গের কর্ণের দৈর্ঘ্য 10 ইউনিট। বর্গটির বাহুর দৈর্ঘ্য কত?
(a) 5 ইউনিট (b) 7 ইউনিট (c) 8 ইউনিট (d) 5√2 ইউনিট
উত্তর: (d) 5√2 ইউনিট